The examples in this section provide an introduction to the use of PEANUTS in fitting proportional hazards models. As noted above, we use the clinical trial data of Feigl. The data set includes three variables for 42 subjects. The variables are a case indicator (coded as 1 for cases and 0 for censored observations); the survival time (in days); and a treatment indicator (coded as 1 or 2). The data are stored in a file called FEIGL.DAT that has one record per case, and the variables are separated by one or more spaces or tabs.
The first five records from this file are:
0 6 1
1 6 1
1 6 1
1 6 1
1 7 1
Example 6.1 Fitting an Exponential Relative Risk Model and Testing for a Treatment Effect
The commands to describe the input data and read the file are
NAMES cases time group @
INPUT ../exdata/feigl.dat @
We begin by fitting the null model, which can be written as
where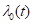 
is an arbitrary, unspecified,
baseline hazard function. In this case there are no covariates. This model
provides a baseline for the likelihood ratio test for the model of primary
interest, which is
in which the parameter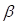 
is the log of the risk of group
2 relative to that of group 1.
The null model is fit using the command
FIT @
The output produced by this command is shown below.
Output 6.1 A null model fit in PEANUTS
FIT @
Hazard function regression
Additive excess relative risk T0 * (1 + T1 + T2 + ...)
cases is used for cases
time is used for survival time
Records used 42
-2 * log-likelihood 187.97 Free parameters 0
AIC 187.97 Informative risk sets 17
In this case the fit summary does not include a parameter summary table because the model contains no covariates. There is also no iteration summary because fitting this model does not require iteration.
The next few lines indicate that this is a hazard function regression model and describe the general form for the current model. This description emphasizes that all PEANUTS models are relative risk models because they describe the risk relative to the unspecified background hazard. Although not illustrated here, a description of the active subset is written if a selection is in effect. The next lines display the name of the time and case key variables. These variables are required for all PEANUTS models. In this example it was not necessary to specify these key variables explicitly because the variables have names recognized by the program. The default names for the time variable are time or exit. The default case variable names are cases, event, or status. As subsequent examples will show, the CASES or EVENT command can be used for explicit specification of the case variable, while the TIME or EXIT command can be used for explicit specification of the exit-time variable.
Because, as noted above, this model contains no regression parameters, there is no parameter summary and only the deviance is presented. The deviance for PEANUTS models is defined as minus two times the log-likelihood (Technical Details contains formulae for the deviance values printed by PEANUTS and the other EPICURE programs). Because the concept of degrees of freedom has no meaning for PEANUTS models, the summary indicates the number of free parameters and risk sets (distinct failure times) in the data.
Example 6.2 Estimating a Treatment Effect and Computing the Likelihood Ratio Test
We continue this analysis by estimating the group effect. In conjunction with this, we will also compute the likelihood ratio statistic for the null hypothesis of no treatment effect.
Because of the general nature of the models available in any of the EPICURE regression programs and the ease with which models can be changed, it is possible that complex reparameterizations are nested, while relatively simple ones are not. For this reason the EPICURE regression programs do not automatically compute likelihood ratio tests. Instead, we have implemented a more flexible approach that requires specification of a base model for comparison and subsequent requests for computation of likelihood ratio tests of interest. The NULL command specifies the base model. This command causes information about the most recent model to be saved for use in the computation of subsequent likelihood ratio tests. The base model can remain unchanged for several subsequent models or it can be changed at any time with another NULL command. The LRT command requests computation of the likelihood ratio statistic and the associated P-value. The statistic is computed as the difference between the deviance for the current model and that for the null model. The degrees of freedom are computed as the difference between the numbers of free parameters for the two models. Although the program checks for consistency between the sign of the deviance change and the degrees of freedom, it is ultimately the user's responsibility to ascertain the validity of any likelihood ratio test.
In this example we first specify the current model, that is, the model fit in the last example, as the base model. We then fit the model with a group effect and request the likelihood ratio test. The commands to do this are
NULL
FIT group @
LRT
The output produced by these commands is shown below.
Output 6.2 A treatment effect model with likelihood ratio test
NULL @
FIT group @
Iter Step Deviance
0 0 187.970
1 0 172.771
2 0 172.759
3 0 172.759
Hazard function regression
Additive excess relative risk T0 * (1 + T1 + T2 + ...)
cases is used for cases
time is used for survival time
Parameter Summary Table
# Name Estimate Std.Err. Test Stat. P value
-- ---------------------------- ---------- --------- ---------- --------
Log-linear term 0
1 group.................... 1.509 0.4096 3.685 < 0.001
Records used 42
-2 * log-likelihood 172.759 Free parameters 1
AIC 174.759 Informative risk sets 17
LRT @
LR statistic 15.21 Degrees of freedom 1
P value < 0.001
The NULL command produces no output. The FIT command is followed by the iteration summary. For each iteration, the program prints a summary of the deviance. The iteration summary also includes information on step halving (discussed in Technical Details). Step halving refers to a modification to the default Newton-Raphson step that occurs whenever the standard step fails to increase the log likelihood (decrease the deviance).
The fit summary begins as in the previous example but includes a parameter summary table. This table has one line for each parameter in the model (in this case there is only a single parameter). The information for each parameter includes
The parameter number, which is needed for some commands, and the name of the covariate associated with the parameter;
The parameter estimate;
The asymptotic standard error of the parameter;
Test statistic and it’s P-value (see Hypothesis Tests and Confidence Bounds for more information);
As illustrated elsewhere in this guide, for more complex models the parameter summary table is divided into sections labeled by the subterm type and term number. In this example, the parameter is in the loglinear subterm of term 0. This is the default subterm for PEANUTS models.
The results from this fit indicate that the risk in group 2 is
or 4.5 times that in group 1.
The likelihood ratio statistic is over 15 with one degree of freedom. This is
highly significant. The CI command can be used to
produce Wald confidence bounds for the treatment effect on both the log and risk
scales. The command to carry out these computations is
CI @
The output produced by this command is shown in Output 6.3.
This table contains the parameter estimate and its standard
error as well as upper and lower 95 percent Wald bounds. (These bounds are
computed as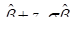 
, where 
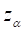is an appropriate normal
deviate.) The level for these or other bounds can be changed with the LEVEL subcommand of the FITOPT or
CI command or with the CI
subcommand of the FITOPT command. This table also
includes the risk estimate and bounds transformed to the risk scale, that is,
.
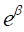Output 6.3 Wald bounds and relative risk estimate for an exponential relative risk model
CI @
95% Confidence Bounds
# Name Estimate Std. Err. Lower Upper
-- ---------------------------- ---------- --------- -------- --------
Log-linear term 0
1 group.................... 1.509 0.4096 0.7065 2.312
EXP(estimate) 4.523 1.506 2.027 10.09
The BOUNDS command can be used to obtain a profile likelihood-based confidence interval for the parameter in this model. The computation of likelihood bounds is computationally intensive, but they have better statistical properties than do Wald bounds. The command to request the computation of likelihood bounds for the treatment effect parameter here is
BOUND 1 @
The number in this command refers to the parameter number from the parameter summary table. The MODEL command can be used to obtain information about the current model, including parameter numbers, without fitting it. This command produces a table like that produced by the fit command but does not fit the model. The output from this command indicates that the 95% likelihood bounds for this parameter are (0.737, 2.362) or on the relative risk scale, (2.09, 10.61). In this example, the Wald and likelihood bounds are quite similar. However, this is not always the case.
Example 6.3 Using Time-Dependent Covariates to Test the Proportional Hazards Assumption
In the final two examples of this section, we will demonstrate the methods for working with time-dependent covariates. In particular, we consider tests of the proportional hazards assumption, that is, that the relative risk is constant over time. Later in this chapter we present additional examples illustrating the use of time-dependent covariates.
We consider two alternatives to the proportional hazards model. In the first, we model the time dependence as a smooth function of time; in the second, we divide the follow-up period into three intervals and estimate a separate treatment effect for each time interval.
The first model can be written as
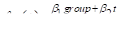
where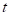 
is the current time, while the
second model is
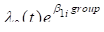
where the subscript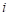 
on the group parameter indexes
time periods. For both models we will compute the likelihood ratio statistic,
comparing the more general model to the model of the last example.
The TTRAN command defines time-dependent covariates. Transformations defined using this command are evaluated for all subjects at each failure time. In defining these transformations, you use a special covariate called %TIME that contains the time at which the transformations are being evaluated.
For the first model we define the time-dependent interaction with the following time-dependent transformation:
TTRAN grt = group
%TIME @
We then indicate that the simple group effect model is to be the base model for the likelihood ratio test, fit the new model, and request a likelihood ratio test with the commands
NULL
FIT + grt @
LRT
Note that we use the + model formula operator to indicate that the previous model is to be updated rather than replaced. The parameter summary and likelihood ratio test result for this model are shown below.
Output 6.4 Test for a time-dependent trend in the relative risk
Hazard function regression with time-dependent covariates
Additive excess relative risk T0 * (1 + T1 + T2 + ...)
cases is used for cases
time is used for survival time
Parameter Summary Table
# Name Estimate Std.Err. Test Stat. P value
-- ---------------------------- ---------- --------- ---------- --------
Log-linear term 0
1 group.................... 1.596 0.7764 2.056 0.0398
2 grt...................... -0.008135 0.06128 -0.1327 > 0.5
Records used 42
-2 * log-likelihood 172.742 Free parameters 2
AIC 176.742 Informative risk sets 17
LRT @
LR statistic 0.01772 Degrees of freedom 1
P value > 0.50
The results suggest that there is little evidence of a smooth trend in the relative risk over time. The point estimate for the interaction term suggests that the risk in group 2 is decreasing at slightly less than 1 percent per unit of time relative to that in group 1.
Example 6.4 Using Time-Dependent Category Variables
In this example, we carry out another test for variation in the relative risk over time based upon the second model described above, in which the risk is not constrained to vary smoothly with time. To do this we will define a time-dependent category variable, that is, a category variable that is a function of %TIME. This category variable, which we will call tcat, will be defined so that roughly one third of the cases occur in each time period.
First, we need to choose cutpoints for this variable. We can do this using the command
QUANTILES time; WEIGHT cases TERTILES @
The WEIGHT option indicates that the cases variable will be used as a weight in ranking the times. Records with non-positive weights are excluded from the ranking. The TERTILES option is used to request display of the 33rd and 66th percentiles. The default display shows quartiles. The output from this command is
Variable: time (with cases as weight variable)
Minimum 1
33.3333% 6
Mean 9.7
66.6667% 11.6667
Maximum 23
Using 30 records : Sum of weights = 30
12 records with zero weight
Using this information we define the tcat variable as
TTRAN tcat = 1 + (%TIME >= 6) + (%TIME >= 12) @
Note that this command does not replace the time-dependent transformations defined previously; it simply adds some additional transformations. The command TTRAN @ removes previously specified time-dependent transformations. The ability to remove time-dependent transformations is important because the program uses the slower time-dependent algorithm whenever TTRAN transformations are defined, even if the model does not contain any time-dependent covariates. It should be noted that covariates defined using the time-dependent transformations are not dropped when this command is given. However, in most cases such variables have little meaning after the relevant transformations have been removed.
The command
TLEVEL tcat @
instructs the program to specify tcat as a categorical variable and to determine the number of levels. The TLEVEL command is necessary here because it forces evaluation of the time-dependent transformations to determine the correct range for the category values. In this example, we let the program determine the number of levels for tcat. However, if you want to specify the number of levels explicitly, either the LEVELS or TLEVEL command can be used. The LEVELS command in this case would be
LEVELS tcat 3 @
We now fit the model and compute the likelihood ratio statistic of interest with the commands
FIT tcatgroup @ LRT
Note that we have replaced the previous model with a step function model and that we used the time-dependent category variable in an interaction as if it were an ordinary variable. Also note that we did not give a NULL command before the fit. This is because the test of interest here compares this model to the model with only the group effect, that is, the base model specified previously. Output 6.5 contains the parameter summary table and likelihood ratio tests for this model.
Output 6.5 A model with a time-dependent category variable
Hazard function regression with time-dependent covariates
Additive excess relative risk T0 * (1 + T1 + T2 + ...)
cases is used for cases
time is used for survival time
Parameter Summary Table
# Name Estimate Std.Err. Test Stat. P value
-- ---------------------------- ---------- --------- ---------- --------
Log-linear term 0
1 tcat_1 * group........... 12.43 150.3 0.08269 > 0.5
2 tcat_2 * group........... 0.6174 0.6068 1.017 0.309
3 tcat_3 * group........... 1.626 0.6553 2.481 0.0131
Records used 42
-2 * log-likelihood 166.366 Free parameters 3
AIC 172.366 Informative risk sets 17
*** WARNING: Parameter tcat_1 * group changed by 8.7% MLE may be infinite or may not exist
LRT @
LR statistic 6.394 Degrees of freedom 2
P value 0.0409
There are several interesting features in these results. First, the likelihood ratio statistic is slightly more than 6 on two degrees of freedom. This is significant at about the 0.05 level and suggests heterogeneity in the risk. Looking at the parameter estimates, we see that the time-period-1 parameter estimate and its standard error are both very large. Indeed, as we will see, the relative risk in this period is infinite, while the risk estimates for the other two time periods are finite. Because this parameter is on the boundary of the parameter space, the Wald statistic is useless, while the likelihood ratio test provides a more accurate assessment of the significance of the differences between the risks across these time periods. Examination of the profile likelihood of the lower likelihood bound for the first parameter would be interesting but will not be carried out here.
To conclude this example, we will use some of the EPICURE analysis commands to examine the temporal distribution of cases by group. In particular we will define categorical variables for group and time period (not time-dependent) and request a case-weighted frequency table. This is accomplished with the following commands:
TRAN gr = group ; tc = 1 + (time 
6) + (time 12) @
LEVEL gr tc @
FREQ gr tc ; WEIGHT cases @
The redefinition of group is done only to avoid having to remove group from the current model before redefining it as a categorical variable. The EPICURE programs do not process LEVELS commands for covariates or stratification variables in the current model. The table produced by these commands is shown below.
Output 6.6 Weighted frequency table output
FREQ gr tc ; WEIGHT cases @
Entries:
Sum of cases
tc
gr | 1 2 3 | Total
-----------+-------------------------------+----------
1 | 0 5 4 | 9
2 | 9 6 6 | 21
-----------+-------------------------------+----------
Total | 9 11 10 | 30
30 records with positive weight
12 records with zero weight
The results in this table indicate that 9 of the 21 failures in group 2 and none of the 9 failures in group 1 occurred during the first 6 days of follow-up.
The FREQ command could be replaced by SUM cases; BY gr tc @ to obtain a listwise rather than a tabular summary.
The examples in this section have used a simple data set to provide an introduction to modeling with PEANUTS. Although only the default exponential relative risk model was used, we have illustrated many features of PEANUTS, including the use of time-dependent covariates and the computation of confidence intervals. The last two examples also illustrated the use of some of the EPICURE analysis commands. Listing 6.1 at the end of this chapter contains a complete listing of the commands used in the examples of this section.