is computed as In working with models, it is important not only to be able to produce parameter estimates but also to be able to test hypotheses about the model and to describe the uncertainty in the estimates. EPICURE provides various methods for hypothesis testing and computing confidence intervals. These procedures are briefly described in this section.
For each model fit, the output includes the parameter estimates, their asymptotic standard errors, and a function of the log likelihood called the deviance. For AMFIT and GMBO/PECAN the deviance (McCullagh and Nelder 1989) is the usual deviance for Poisson and binomial generalized linear models, respectively. For these programs the degrees of freedom are computed as the number of records used in the current analysis minus the number of free parameters (including strata parameters) in the model. For conditional logistic regression models in GMBO/PECAN and hazard function models in PEANUTS the reported “deviance'' is minus twice the log likelihood. Because there is no analog of degrees of freedom for these models, the output includes information on the number of free parameters and the number of informative risk sets. Informative risk sets are defined as risk sets that make a positive contribution to the information matrix. For example, in a conditional logistic regression model with an exposure effect, risk sets in which all cases and controls have the same exposure provide no information for parameter estimation.
There are three standard procedures for testing hypotheses about models fit using maximum likelihood methods. These procedures are the Wald test, the score test, and the likelihood ratio test. All three tests are available in EPICURE. Each procedure can be used as the basis for construction of confidence intervals.
The Wald statistic for a null hypothesis of the form is computed as
Symmetric α-level Wald-based confidence bounds for a single parameter are computed as
where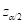 
is the upper
100α/2 percentile of a standard normal distribution.
Wald-based confidence bounds for each of the free parameters in a model can be requested with the CI command or the CI fit option (described in Using the FITOPT Command to Control the Fit). The Wald confidence bound table includes the upper and lower Wald bounds for each parameter in the model and for parameters in log-linear subterms. The table also shows the exponentiated estimate and bounds. Although Wald tests and Wald-based confidence bounds are commonly used, score and likelihood ratio tests have better statistical properties and are generally preferable to Wald tests, particularly for nonstandard (non-exponential) models. The LINCOMB command can be used to compute Wald bounds for linear combinations of model parameters.
Standardized score statistics are simpler to compute than
likelihood ratio tests because they can be computed with only a single pass
through the data. Under the null hypothesis, score statistics are asymptotically
distributed as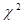 
random variables. Rao (Rao
1948) and Cox and Hinkley (Cox and
Hinckley 1974) discuss score statistics and other aspects of
likelihood estimation in detail. Additional details will not be presented
here.
Output 4.1 contains the EPICURE parameter summary table for a logistic regression model used in Example 5.3 to illustrate some features of GMBO/PECAN. The summary table provides information on the covariate associated with each parameter along with the parameter estimate and its estimated standard error. The Test Stat. and P value columns give the Wald test and it’s P-value for parameters that have been estimated (parameters 1, 3, and 4 in this model). This is a test of the null hypothesis that the parameter is 0. For parameters whose value was fixed for this analyses (such as parameters 2 and 5 in this example) test statistic is the signed square root of score statistic. This is an asymptotically normal statistic that can be used to test of the hypothesis that the true value of the parameter is equal to the assigned value. The sign is determined by the sign of the score (first derivative of the log-likelihood with respect to the parameter).
Output 4.1 Parameter summary table
kyphosis is used for cases
Bernoulli trials
Parameter Summary Table
# Name Estimate Std.Err. Test Stat. P value
-- ---------------------------- ---------- --------- ---------- --------
Log-linear term 0
1 %CON..................... -0.8043 1.159 -0.6938 0.488
2 age...................... 0.000 Fixed 1.098 0.272
3 number................... 0.3039 0.1763 1.724 0.0848
4 start.................... -0.1879 0.06421 -2.926 0.00343
5 age * age................ 0.000 Fixed 0.0754 > 0.5
The SCORE command can be used to compute the score test for sets of parameters. The syntax of the SCORE command is similar to that of the FIT command in that a model formula that updates the current default subterm can be included in the command. However, the model formula on a SCORE command is always used to update the subterm. It is important to remember that the score statistic produced by this command is the score statistic for the free parameters in the model. It is possible to compute score-based confidence intervals for specific parameters (Miettinen 1976, Gilbert 1989); however, EPICURE does not provide a direct mechanism for these computations. The facilities for the computation of likelihood-based bounds obviate the need for the poorer score-based intervals.
Likelihood ratio tests for nested models are computed as twice
the difference in the log likelihood for the models being compared. (Two models
are said to be nested if the free parameters in the more-restricted model are a
subset of the free parameters in the less-restricted model.) In EPICURE the likelihood
ratio statistic is computed as the difference in deviance for the models being
compared. This difference is asymptotically distributed as a 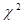random variable with degrees of
freedom equal to the difference in the number of parameters for the two
models.
The NULL and LRT commands are used to carry out likelihood ratio tests. The NULL command is used to designate the most recently fit model as the “null model”. This is the model that will be used as the basis for comparisons in subsequent tests. After a subsequent model has been fit, the LRT command is used to request computation of the likelihood ratio test. Following this command, the deviance for the current model is subtracted from that of the null model, and the difference in the number of free parameters in the two models is computed. If there is no null model, or if there is an inconsistency between the value of the test statistic and its degrees of freedom, an error message is printed. Tests can be computed for either the addition or deletion of covariates. The deletion of covariates is indicated by negative values for the degrees of freedom and test statistic. (Because of this feature the “null model” may actually represent an alternative hypothesis.) For valid tests the program prints the test statistic, its degrees of freedom, and the P-value. An error message is printed for invalid tests. It is important to remember that it is ultimately the user's responsibility to ensure the validity of a test, that is, that the models being compared are actually nested. Because of the general nature of the models in EPICURE, it is not possible for the program to determine if a specific comparison involves nested models.
It is possible to define confidence bounds in terms of the
profile likelihood (Moolgavkar
and Venzon 1987, Venzon
and Moolgavkar 1988) , which is the
likelihood considered as a function of the parameter(s) for which the bound is
sought. If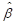 
denotes the maximum likelihood
estimate of a single parameter, 
, then the 
-level likelihood-based lower bound
for is a value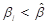 
such that 
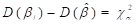, where 
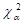is the appropriate
percentile of the single degree-of-freedom 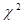distribution. The upper
likelihood bound is defined analogously. Likelihood-based bounds can be computed
with the BOUNDS command,
which makes use of the algorithm proposed in (Venzon
and Moolgavkar 1988) to find profile likelihood bounds for specific
parameters.
In general, likelihood ratio tests and likelihood-based confidence bounds are the preferred method for testing and estimation, especially in nonstandard models. However, these methods are computationally intensive and, in some cases, likelihood-based bounds may not exist because of restrictions on the ranges of the parameters.
EPICURE has two commands, BOUNDS and PROFILE, for computing confidence limits or specific parameters based on the shape of the profile likelihood. The basic syntax for these commands is
BOUNDS # @
and
PROFILE # @
where # is the number of the parameter in the current model for which a bound is desired. By default the BOUNDS command computes upper and lower confidence bounds at the current default significance level using the Moolgavkar-Venson algorithm (Venzon and Moolgavkar 1988) with some refinements to improve performance. The PROFILE command uses a direct search to estimate bounds (of they exist) at a set of confidence levels with two-sided levels of 25%, 50%, 68.3%, 75%, 90%, 95%, 97.5%, 99%, and 99.5%. The PROFILE command also produces a plot of the profile likelihood along with a curve summarizing the Wald bounds. Output 4.2 contains the table of bounds produced by a PROFILE command and the profile likelihood bounds. In the plot the points are the likelihood bounds and the blue curve is a locally-quadratic fit to the points. The dashed magenta line indicates the pattern of the Wald bounds. The vertical axis gives the absolute change (decrease) in the deviance relative to it’s maximum value. The deviance drop for a 95% confidence interval is 3.84.
Output 4.2 Likelihood based bounds with profile likelihood plot
Interpolated profile likelihood bounds
for parameter 9 (dgy)
MLE 0.4654
2-sided Bounds
Level Lower Upper
________________________________
25.0% 0.3363 0.6037
50.0% 0.1972 0.7627
68.3% 0.07780 0.9169
75.0% 0.02502 0.9905
90.0% -0.1383 1.243
95.0% -0.2336 1.413
97.5% -0.3125 1.571
99.0% -0.3978 1.766
99.5% -0.4503 1.906
The UPPER and LOWER subcommands can be used to limit the computations to upper or lower bounds, respectively. If this is done, the bounds will be the same as that computed if both upper and lower bounds had been requested. Thus, if the default level is 95 percent, the tail probability for each bound would be 0.025. The BOTH subcommand can be used to override the effect of the selection of a specific bound. The LEVEL subcommand can be used to change the default confidence level for the BOUND command. (This will also change the level in subsequent Wald bound computations.) The GOAL subcommand can be used to override the current confidence level by specification of a specific value for the deviance at the bound. The goal deviance must be larger than the current deviance. This option is useful in the computation of confidence regions in two or more dimensions or in some cases where an initial attempt to compute a bound fails.
There are situations in which these commands fail to compute some bounds. The PROFILE command provides more information and, while requiring more computations, is more robust than the BOUNDS command, especially when the profile likelihood changes rapidly as a function of the parameter of interest. Constraints, either implicit or explicit, on the range of a parameter are among the most common reasons for the failure of these commands. This type of failure is usually indicated by an error message indicating that no feasible value could be found. The following examples illustrate the most common reasons for this type of failure. Consider two parameterizations of a product additive excess risk model,
and
As long as the maximum likelihood estimate (MLE) of 
is positive, we can
estimate this parameter (or its logarithm) using either form of the model.
However, even if the MLE of is positive, it
is possible that the lower likelihood bound is negative. If this is the case, it
will be impossible to compute this bound using the first parameterization. In
models such as the hazard function models in AMFIT or PEANUTS or the odds ratio models in GMBO/PECAN, the hazard
function or odds ratio must be positive. This imposes an implicit constraint
that be greater than 
over the maximum value of the
dose variable. If the profile likelihood in the limit as the parameter
approaches its bound is not sufficiently small (that is, the deviance is not
sufficiently large), then the desired bound does not exist.
If you have doubts about the likelihood ratio bounds reported by a program, they can be checked quite easily. The lower and upper bounds at the default level are saved in named constants called, respectively, #_lrlo and #_lrhi. By fixing the parameter of interest at one of these values, fitting the model, and computing the likelihood ratio statistic for the resulting model, you can verify that the bounds are correct. The following commands show how this could be done:
FIT @
NULL
BOUNDS 2 @
! Check the lower bound
PARA 2=#_lrlo @
FIT @ LRT
! Now check the upper bound
PARA 2=#_lrhi @
FIT @ LRT
The P-value for the likelihood ratio tests in this example will be equal to 1 minus the default level if the bounds are correct.
The likelihood bound computations may also fail when the likelihood is very flat in one direction. This problem is usually indicated by a warning message noting that, even though convergence in deviance appeared to have been achieved, the score was larger than expected. This problem can sometimes be overcome by reparameterization. It may also be possible to use the GOAL subcommand to find the bound. Consider a model in which the deviance at the MLE is 1000.00 and we are attempting to find the 95 percent upper bound for parameter 2. The deviance at this bound should be 1003.842. We begin with the following commands to fit the model and attempt computation of the upper bound:
FIT @
BOUNDS 2 @
If the large score message appears, we can make a second attempt to find the bound using the following commands:
PARA 2=#_lrhi @
FIT @
BOUNDS 2 FORCE UPPER GOAL 1003.842 @
The FORCE subcommand is used to force the computation of the bound even though the parameter of interest was fixed in the last model fit. The GOAL subcommand indicates the value of the likelihood we want to achieve. If this attempt fails, we could of course repeat the process, but in general we will have learned enough at this point to seek an alternative parameterization (if possible), or we can report that the likelihood was flat and no bound was found.
As shown in several examples in the following chapters, despite the dire problems discussed above, the likelihood bounds can usually be found without problems.