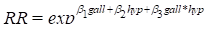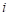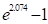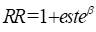Stratified models for the odds ratio – matched case control studies

This section contains examples that illustrate the use of GMBO/PECAN to fit stratified models for the odds ratio.  The primary focus here is on the analysis of matched case control studies using conditional logisticregression, but one can also fit stratified models using unconditional logistic regression.  The latter approach is useful, and is the EPICURE default choice, for strata (case-contral sets) with large (more than 50 by deafult) individuals. 

The data used  for most of the examples originated in a matched case-control study of the effect of exogenous estrogens on the risk of endometrial cancer among women in a retirement community near Los Angeles (Mack, Pike et al. 1976). The study incldued  63 cases with 4 matched controls per case. Matching was made on the basis of age (within one year), vital status and community of residence at the time of diagnosis of the case, age at entry into the retirement community, and marital status. Women who had a hysterectomy prior to the time at which the case was diagnosed were not considered as controls. The analysis of these data have been discussed in detail by Breslow and Day (Breslow and Day 1980).

The variables in this data set are

The case-control indicator is coded 1 for cases and 0 for controls. The other indicator variables are coded 1 for yes and 0 for no. Conjugated estrogen dose is coded as 0 for none, 1 for -0.1 -0.299 mg/day, 2 for 0.3 -0.625 mg/day, and 3 for 0.6325 or more mg/day. Data on obesity, estrogen dose, and estrogen usage duration were missing for some women. Missing values for these variables are coded as 9, 9, and 99, respectively. The data are sorted by set number, and within each set the case is the first.

Example 5.11         Matched Case-Control Data with 1:1 Matching

For this example, we will reproduce some of the analyses described in Section 7.3 of Breslow and Day (Breslow and Day 1980). These analyses make use of 63 case-control pairs consisting of the case and first control from each matched set in the data set. Transformations will be used to create a variable that is used to select desired records.

The commands used to read the input data (which are assumed to be stored in a text file suitable for free-format input) and create some additional variables needed for the analyses are

NAMES setno cases gall hyp ob est cdose dura non age @

INPUT ../exdata/leimod.dat@

MISS cdose 9; ob 9; dura 99 @

CONS #cage = -1 @

TRAN IF cases == 1 THEN

   #cage = age ;

 ENDIF ;

 cage = #cage ;

 categ = 1 + (cage >= 65) + (cage >= 75) ;

 cage70 = cage - 70 ; agegp = (age >= 70) ;

 cest = (cdose > 0) ;

 caseno = GL(5,1) ; pairs = caseno <= 2 ;

     @

     SAVE @

The data are read from a file called LEIMOD.DAT. The MISS command is used to recode missing values for dose, ob, and dura to the EPICURE missing value code. The constant transformation is used to initialize the named constant (#cage) needed for computation of the special age variable (cage) used in many of the Breslow and Day analyses. This variable is defined to be the age of the case in each matched set.

The GL function generates a sequence of regular labels. In this case there are five labels and each label is repeated one time, resulting in the sequence 1, 2, 3, 4, 5, 1 ,2, 3, 4, 5, . Because of the way in which the data are sorted, the value of caseno is 1 for the cases and 2 for the first control for each case. The pairs variable is an indicator used to select records for the initial analyses. The data are saved in a BSF file with the default name, LEIMOD.BSF.

Since the analyses in this example will use only one control per case, we select those cases with pairs equal to 1. This is accomplished with the command

SELECT pairs == 1 @

Although it is not necessary for this example because the default names are used, we explicitly specify the case-control indicator and set-number variables using the commands. The COND command instructs the program to use conditional likelihood.

CASES cases

STRATA setno@

COND @

We continue this example by reproducing some of the results described in Table 7.3 of (Breslow and Day 1980). The first model to be considered is a model with no covariates, that is, a model in which none of the covariates have an effect on the cancer risk. The NULL command is given after the fit to designate this model as the null model for a subsequent likelihood ratio test. This will create named constants called #_nuldv and #_nulnp, which contain the deviance and degrees of freedom, respectively, for this model. We also use constant transformations to save another copy of the deviance for this model in a named constants called #basdv for use in later computations. The commands to fit this simple model and save the deviance are

FIT @

NULL

CONS #basdv = #_dv @

We will now compute score and likelihood ratio tests for an effect of estrogen usage on the risk of endometrial cancer. The risk model used here is the usual log-linear model

After computation of the score test, we fit the model and compute the likelihood ratio test of the null hypothesis that estrogen usage has no effect on the risk of endometrial cancer. In addition, we compute the Wald confidence bounds (this also displays the relative risk estimate). This is done using the following commands:

SCORE + est @

FIT @

LRT

CI @

The SCORE command updates the model and computes the score statistic for the null hypothesis that estrogens have no effect on the risk of endometrial cancer. The FIT command is used to fit the updated model, and CI causes 95 percent Wald bounds to be computed and displayed. The LRT command instructs the program to compute and display the likelihood ratio test. The output produced by these commands is shown in Output 5.11.

The summary for the fitted model differs slightly from that for an unstratifeid model. The model description and parameter summary table are essentially identical. However, the deviance summary is different. In EPICURE the “deviance” for conditional logistic regression models is defined as minus two times the log-likelihood. This is identical to the goodness-of-fit () statistic of Breslow and Day  (Breslow and Day 1980). Defining the deviance in this way means that the likelihood ratio statistic for the comparison of nested models can be computed simply as the difference between the deviance values for the two fits with degrees of freedom equal to the difference in the number of free parameters in the model. The PECAN deviance summary also includes the number of free parameters in the model, the number of risk sets used in the analysis, and the number of non-informative risk sets. Non-informative risk sets are those risk sets in which the cases and controls have the same pattern for all covariates in the model. In this model, there are 31 case-control pairs in which both the case and control used or did not use estrogens and, thus, provide no information for the estimation of the odds ratio non-informative.

Output 5.11  Estimation and testing for an estrogen effect on endometrial cancer risk-1:1 matching

FIT @

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

            Records used          126

                Deviance      87.3365         Free parameters       0

                                            Informative strata     63 (handled with the conditional likelihood)

NULL

CONS #basdv = #_dv @

SCORE + est @

The score statistic is 21.125 with df = 1 (P  < 0.001 )

FIT @

          Iter  Step      Deviance

             0     0      87.3365

             1     0      64.2288

             2     0      62.9341

             3     0      62.8875

             4     0      62.8874

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 est......................          2.269      0.6065      3.741    < 0.001

            Records used          126

                Deviance      62.8874         Free parameters       1

                                            Informative strata     32 (handled with the conditional likelihood)

                                        Non-Informative strata     31

LRT

             LR statistic       24.45      Degrees of freedom      1

                  P value     < 0.001

CI @

                                       95% Confidence Bounds

 # Name                           Estimate    Std. Err.      Lower       Upper

-- ----------------------------  ----------   ---------    --------    --------

Log-linear term 0

 1 est......................         2.269     0.6065     1.080     3.457

             EXP(estimate)            9.667       1.834       2.945       31.73

The next set of commands are used to fit a set of nested models for the effects of gallbladder disease, hypertension, and the joint effect of having had both of these conditions on endometrial cancer risk. The models to be used in these analyses are all contained in the following model:

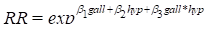
Before fitting the gallbladder model, we compute a score statistic for the gallbladder disease effect. This could be done in a similar way for the subsequent models. After the first fit, we use the LRT command to compute the likelihood ratio statistic and then save the information about the current fit for use as the null model in the next test. After the final test, we explicitly compute the two degree-of-freedom likelihood ratio test comparing the full model to the model with no parameters and use the CHISQ command to evaluate the P-value for this test. If we had not given the NULL command after the first fit, the LRT command could have been used to compute this statistic and the associated P-value. However, since the null model was changed, it is necessary to compute the test statistic and its associated P-value explicitly. This computation makes use of the #basdv constant saved earlier. The commands to fit these models and carry out the tests of interest are

NOMODEL

FIT @

SCORE + gall @

FIT @ LRT

NULL

SCORE +hyp @

FIT @

LRT NULL

CONS #dvdif = #basdv - #_dv @

CHISQ 2 #dvdif @

FIT + gall*hyp @ LRT

This series of commands is generally straightforward; however, you should note the use of the NOMODEL command to clear the previous model. This command removes all parameters currently in the model. (This could also be accomplished with the LOGL 0 @ command.) This is done here only because we wish to compute the score test. A portion of the output produced by these commands is shown below.

Output 5.12  Output (partial) for estimation and testing for the effects of gallbladder disease and hypertension on the risk of endometrial cancer - 1:1 matching

NOMODEL

FIT @

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

            Records used          126

                Deviance      87.3365         Free parameters       0

                                            Informative strata     63 (handled with the conditional likelihood)

SCORE + gall @

The score statistic is 3.55556 with df = 1 (P  =     0.0593)

FIT @

          Iter  Step      Deviance

             0     0      87.3365

             1     0      83.6698

             2     0      83.6536

             3     0      83.6536

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 gall.....................         0.9555      0.5262      1.816     0.0694

            Records used          126

                Deviance      83.6536         Free parameters       1

                                            Informative strata     18 (handled with the conditional likelihood)

                                        Non-Informative strata     45

LRT

             LR statistic       3.683      Degrees of freedom      1

                  P value      0.0550

NULL

SCORE +hyp @

The score statistic is 0.861336 with df = 1 (P  =      0.353)

FIT @

          Iter  Step      Deviance

             0     0      83.6536

             1     0      82.7887

             2     0      82.7878

             3     0      82.7878

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 gall.....................         0.9704      0.5307      1.828     0.0675

 2 hyp......................         0.3481       0.377     0.9233      0.356

            Records used          126

                Deviance      82.7878         Free parameters       2

                                            Informative strata     39 (handled with the conditional likelihood)

                                        Non-Informative strata     24

LRT

             LR statistic      0.8657      Degrees of freedom      1

                  P value       0.352

NULL

CONS #dvdif = #basdv - #_dv @

CHISQ 2 #dvdif @

Chi square = 4.5487 df = 2 P = 0.102864

FIT + gall*hyp @

          Iter  Step      Deviance

             0     0      82.7878

             1     0      80.8714

             2     0      80.8413

             3     0      80.8413

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

Using pairs == 1

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 gall.....................          1.517       0.699       2.17       0.03

 2 hyp......................         0.6270      0.4353       1.44       0.15

 3 gall * hyp...............         -1.548       1.125     -1.377      0.169

            Records used          126

                Deviance      80.8413         Free parameters       3

                                            Informative strata     39 (handled with the conditional likelihood)

                                        Non-Informative strata     24

LRT

             LR statistic       1.947      Degrees of freedom      1

                  P value       0.163

We conclude this example with a categorical model for the estrogen dose-response function. The model can be written as

where 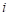 indexes the three conjugated estrogen dose groups for exposed women (group 0 corresponds to unexposed women). To fit this model, we first use the LEVELS command to indicate that cdose is to be treated as a categorical variable. The model is then fit in the usual way. The commands to carry out this analysis are

LEVELS cdose @

FIT cdose @

The output for this model is shown in Output 5.13.

Earlier we noted that information on conjugated estrogen dose was not available for all women in the study and used the MISS command to recode the missing values to the EPICURE missing value internal code. Only those case-control pairs in which both the case and her matched control have nonmissing values for cdose should be used in the analysis. If you look at the deviance summary in the figure, you will see that the number of risk sets is given as 59, which is the number of case-control pairs for which both women have known values for cdose. As a model is fit, PECAN, like all of the EPICURE regression programs, checks the variables involved in the fit for missing values and automatically excludes those records with missing data. For PECAN, this also involves checking whether a risk set can still be included in the analysis. Additional topics related to missing values will be explored further in the next example. The complete set of commands used in this example is shown in Listing 5.3 at the end of this chapter.

Output 5.13  A categorical dose-response model - 1:1 Matching

LEVELS cdose @

cdose has 4 levels from 0 to 3

FIT cdose@

          Iter  Step      Deviance

             0     0      81.7914

             1     0      63.5681

             2     0      62.9863

             3     0      62.9796

             4     0      62.9796

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 59 strata

  Conditional likelihood used for 59 strata

Using pairs == 1

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 2 cdose_1..................          1.524      0.6181      2.466     0.0137

 3 cdose_2..................          1.266       0.569      2.225     0.0261

 4 cdose_3..................          2.120       0.693      3.059    0.00222

            Records used          122          Unused records       4

                Deviance      62.9796         Free parameters       3

                                            Informative strata     45 (handled with the conditional likelihood)

                                        Non-Informative strata     14

Example 5.12         Matched Case-Control Data with 1:M Matching

In the previous example, we considered a subset of the endometrial study data in which the data were limited to the first matched control for each case. In this example, we continue to work with the endometrial cancer data, but we use all of the data, that is, four controls per case. Because PECAN automatically detects 1:M or N:M (multiple cases and controls in each stratum) matching and chooses the appropriate estimation algorithm, it is not necessary for the user to do anything special when working with such data. The commands to read the data are identical to those used in the previous example and will not be repeated here. (One could carry out all of the analyses described in this example in the same session as the analyses of the first example by canceling the selection used to restrict the data to 1:1 matching with the NOSELECT@ or SELECT@ command.)

We begin by fitting the null model, which assumes an odds ratio of 1 in each matched set, and then we consider the model with a multiplicative estrogen effect. The deviance for the null model is saved for use in the computation of likelihood ratio tests and P-values. After computation of the score statistic for an estrogen effect, we fit the estrogen effect model and compute the likelihood ratio statistic (using the script file discussed above). The commands to fit these models and carry out these tests are

FIT @ NULL

SCORE +est @

FIT @ LRT

The output from this analysis is shown below.

Output 5.14  Output from fit of null model and estrogen effect model

FIT@

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

    cases is used for cases

            Records used          315

                Deviance      202.789         Free parameters       0

                                            Informative strata     63 (handled with the conditional likelihood)

NULL

SCORE +est @

The score statistic is 31.1556 with df = 1 (P  < 0.001 )

FIT @

          Iter  Step      Deviance

             0     0      202.789

             1     0      168.806

             2     0      167.462

             3     0      167.443

             4     0      167.443

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 est......................          2.074      0.4208      4.928    < 0.001

            Records used          315

                Deviance      167.443         Free parameters       1

                                            Informative strata     58 (handled with the conditional likelihood)

                                        Non-Informative strata      5

LRT

             LR statistic       35.35      Degrees of freedom      1

                  P value     < 0.001

The format of the parameter summary table is identical to that in the previous example. The point estimate of the log of the relative risk for estrogen exposure, 2.074, is similar to that obtained in the restricted data set of the previous example (2.269), but, because of the use of the additional data, the standard error is about 30 percent less in the current analysis. Also, the number of non-informative risk sets is much smaller in the full data set (5 sets) than it was in the 1:1 matched data (31 sets).

Thus far all of the PECAN examples have made use of the classic linear model for the log of the relative risk. We will now consider an alternative but, in this simple case, equivalent model in which the relative risk is modeled as a linear function of estrogen usage. The model is

The commands to specify and fit this model are

NOMODEL

LINE 1 est @

FIT @

The first command resets the model, which in this case involves removing the parameter associated with est from the log-linear subterm of term 0, and is equivalent to a LOGL 0 @ command. If the previous model contained parameters in several terms or subterms, the NOMODEL command provides a convenient alternative to a series of empty subterm specification commands. The model of interest is specified with the LINE 1 command and fit with the FIT command. The parameter summary table for this fit is shown below.

Output 5.15  Excess relative risk model with matched case-control data

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Stratification on setno with 63 strata

  Conditional likelihood used for 63 strata

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Linear term 1

 1 est......................          6.955       3.348      2.078     0.0377

            Records used          315

                Deviance      167.443         Free parameters       1

                                            Informative strata     58 (handled with the conditional likelihood)

                                        Non-Informative strata      5

Because est is a binary indicator variable, the deviance for this fit is identical to the previous model. The parameter estimate, 6.955, is equal to 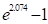, where 2.074 is the estimate of the log relative risk in the log-linear (multiplicative) risk model. Note that the standard error for the excess relative risk parameter is larger than we would expect based upon the P-value for the likelihood ratio test, P <0.001. (This test is identical to that carried out for the log-linear model.) This is a consequence of the parameterization (called parameter effects curvature in modern, nonlinear regression literature) and indicates that one should not rely on the Wald statistic  as a test for the statistical significance of the estrogen effect in this model. It also indicates that Wald-type confidence intervals for this parameterization are misleading. These issues were discussed in detail in the GMBO/PECAN examples. One might obtain a better asymptotic description of the variability in the excess relative risk by estimating the logarithm of the excess relative risk using the model

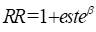
which could be specified and fit with the commands

LINE 1 est=1 @

LOGL 1 %CON @

FIT @

As discussed above and in the GMBO/PECAN examples, likelihood-based confidence bounds provide a useful parameterization-independent description of the variability in specific parameters (for equivalent models). The BOUNDS command can be used to compute likelihood-based bounds for parameters in all EPICURE regression programs. The 95 percent likelihood bounds for the parameter in this linear model are (2.71, 18.78) while those for the log-linear model are (1.00, 2.93). You can easily check the equivalence of these bounds.

Despite potential asymmetry in the likelihood surface, alternative parameterizations such as those considered here are useful in some problems. For example, if one is interested in dose-response models over a broad range of exposures, it may be that the relative risk is better modeled as a linear rather than log-linear function of dose. It may also be the case that effects of factors that modify the risk are better modeled as effects on the excess relative risk than as multiplicative effects on the relative risk.

We continue this example with an illustration of hypothesis tests in the presence of missing values in some of the covariates of interest. In particular, we will consider testing for a log-linear effect of conjugated estrogen dose, cest, on the risk of endometrial cancer. After clearing the previous linear model, one might use the commands

FIT @

FIT cest @

However, since conjugated estrogen dose is not available for all women, the difference in the deviance for these two models is not a valid likelihood ratio test for the estrogen dose response. The null model will be fit using data on all women in the study (315 women in 63 matched sets), but the dose response model will be based upon the data for the 291 women in 59 matched sets with complete dose information. If the fact that estrogen dose is missing is not related to subsequent cancer development, one can construct a valid likelihood ratio test based on an analysis of the subset of women with dose information. The CHECKMISS command can be used to indicate one or more variables to be checked for missing values prior to fitting each model. Records with missing values for any of the variables in the check list are not included in subsequent analyses. Thus, we can use the following commands to fit the null and full models in this example:

CHECK cest @

FIT @

FIT cest @

The output produced by these commands is summarized in below.

Output 5.16  Likelihood ratio test with listwise deletion of records with missing data

CHECK cest @

8 records rejected (in addition to the SELECT)

FIT @

          Iter  Step      Deviance

             0     0      159.223

             1     0      159.223

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Using records with no missing values for:  cest

Stratification on setno with 59 strata

  Conditional likelihood used for 59 strata

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 cest.....................          1.710      0.3541       4.83    < 0.001

            Records used          307          Unused records       8

                Deviance      159.223         Free parameters       1

                                            Informative strata     56 (handled with the conditional likelihood)

                                        Non-Informative strata      3

FIT cest @

          Iter  Step      Deviance

             0     0      188.129

             1     0      159.498

             2     0      159.224

             3     0      159.223

             4     0      159.223

Conditional-logistic regression

Additive excess relative risk T0 * (1 + T1 + T2 + ...)

Using records with no missing values for:  cest

Stratification on setno with 59 strata

  Conditional likelihood used for 59 strata

    cases is used for cases

                            Parameter Summary Table

 # Name                            Estimate     Std.Err.  Test Stat.  P value

-- ----------------------------   ----------   ---------  ----------  --------

Log-linear term 0

 1 cest.....................          1.710      0.3541       4.83    < 0.001

            Records used          307          Unused records       8

                Deviance      159.223         Free parameters       1

                                            Informative strata     56 (handled with the conditional likelihood)

                                        Non-Informative strata      3

Based on the large change in the deviance, it is clear that there is a dose response, with the risk changing by a factor of 5.5 per unit of coded estrogen dose.

The commands for this example are shown in Listing 5.4 at the end of the chapter.