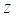is modeled as PEANUTS is used for analysis of ungrouped,
possibly censored survival data using partial likelihood methods for
distribution-free hazard function models, often called proportional hazards
models (Cox
1972, Breslow
and Day 1988). Under this model, the hazard function for an
individual with covariate value 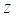is modeled as
where λ0(t) is the baseline or background rate (hazard) and f(β,z) is the relative risk function. If the covariables do not depend on t, this is a proportional hazards model. In PEANUTS you may define covariates that depend on time through the use of special time-dependent transformations (TTRAN command) that can make full use of EPICURE transformations and functions. Stratified models in which the baseline hazard is allowed to vary from stratum to stratum are easily fit with PEANUTS. The program also allows for late entry into follow-up studies (left truncation). Plots of the estimated underlying hazard λ0(t) with optional smoothing are provided. Plots of the integrated hazard or survival function can also be obtained. The plot data can also be saved for use in more powerful graphics programs such as R or Stata.
PEANUTS can be used for fitting models to case-cohort data (Prentice 1986) using the methods described by Therneau (Therneau and Hongzhe 1999) and further developed by Langholz and Jiao (Langholz and Jiao 2007). Case-cohort studies make use of a subset of the full cohort that includes, possibly stratified, sample of the full cohort with known sampling weights and all cases.
Data are read into PEANUTS as individual records. The key variables for standard analyses are the event-time, and an indicator coded as 1 for cases and 0 for censored observations. For left truncated data, an additional key variable containing the entry time is required. For case cohort analyses the data must include a variable that can be used to identify cases that are not in the sampled subcohort.