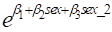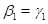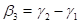Categorical variables may also be used to define interactions
in a model formula on a FIT command. Assuming the
categories are numbered from 1 to n, if the interaction involves one
categorical and one continuous (noncategorical) variable, the model includes a
parameter for each level of the categorical variable. For a subject in the  category, the
category, the  covariate is equal to the value
of the continuous covariate for the subject, and all of the other covariates are
zero. If both variables in an interaction are categorical with
covariate is equal to the value
of the continuous covariate for the subject, and all of the other covariates are
zero. If both variables in an interaction are categorical with 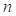 and
and  levels, respectively, a total of
nm covariates are added to the model. For a subject in which the first
categorical variable has the value
levels, respectively, a total of
nm covariates are added to the model. For a subject in which the first
categorical variable has the value  and the second
and the second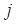 , the
, the 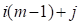 covariate is 1 and the remaining
covariate is 1 and the remaining
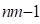 are zero. The indicator
variables used when a categorical variable is included in a fit are created for
each subject as the model is fit. Since these covariates do not use any of the
data workspace, they will be called virtual covariates. The names for virtual
covariates are generated by the programs. These names include the categorical
variable name and a numeric suffix that indicates the level.
are zero. The indicator
variables used when a categorical variable is included in a fit are created for
each subject as the model is fit. Since these covariates do not use any of the
data workspace, they will be called virtual covariates. The names for virtual
covariates are generated by the programs. These names include the categorical
variable name and a numeric suffix that indicates the level.
The model formula initialization operators (= and :) may be
used with categorical variables or interactions involving categorical variables.
In these cases the specified initial value applies to all parameters associated
with the categorical variable. The PARAMETER command
can be used to initialize specific parameters associated with a categorical
variable.
When working with categorical variables, it may happen that
some of the parameters are redundant, or aliased. For example, if sex is a
categorical variable with two levels, the models
 (4.4)
(4.4)
and
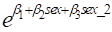 (4.5)
(4.5)
are equivalent. In any of the EPICURE regression programs, these models
could be specified and fit using the commands FIT sex@ and FIT
%CON sex@, respectively. The latter model contains a redundant
parameter.
In this and most similar cases, EPICURE detects this form of
aliasing, called intrinsic aliasing, before fitting the model and automatically
drops one of the covariates from the model. In this example,  would be set equal to 0 and not
be allowed to vary during the maximization, in which case the relationship
between the parameters in the two models is
would be set equal to 0 and not
be allowed to vary during the maximization, in which case the relationship
between the parameters in the two models is 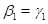 and
and 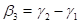 .
.
In general, when EPICURE detects intrinsic aliasing, the
parameters associated with the lowest levels of the categorical variables
involved will be dropped. This method is similar to that used in GLIM, but it
differs from the SAS approach. The default choice can be overridden by
explicitly fixing the parameters associated with the parameters to be omitted
from the model. This is done using the PARAMETER command as illustrated in the
following examples. If a model contains aliased parameters that are not detected
prior to fitting, they will be detected as the model is fit. This type of
aliasing is called extrinsic aliasing. Extrinsic aliasing occurs when one
parameter is a linear combination or a (1-1) function of other parameters in the
model. The parameter summary for a fitted model indicates any aliased parameters
detected during a fit.
We will use models (4.4) and (4.5) to make this discussion more
concrete. If sex is a categorical variable, model (4.4) could be specified with
the command
FIT sex @
This model contains no redundant parameters. On the other hand,
the command
FIT %CON sex @
specifies model (4.5), which is equivalent to model (4.4) but
includes a redundant parameter. Using its standard rules, the program determines
that there is an extra parameter and drops the sex_1 parameter from the model
(and the output summary). However, if the command
PARAMETER 3=0 @
used to fix the parameter associated with sex_2 at 0, the sex_1
parameter will be included in the model. The first argument in this command is
the parameter number; the  operator is followed by
the initial value. This operator is used to indicate that the indicated
parameter is to be treated as fixed at the specified value throughout the
iterations. The other PARAMETER command operators are
:, >, and <, which indicate initialization without fixing,
parameter minima, and parameter maxima, respectively. The parameter number can
be obtained from the parameter summary table printed after a fit or from the
model summary table printed after the MODEL command.
operator is followed by
the initial value. This operator is used to indicate that the indicated
parameter is to be treated as fixed at the specified value throughout the
iterations. The other PARAMETER command operators are
:, >, and <, which indicate initialization without fixing,
parameter minima, and parameter maxima, respectively. The parameter number can
be obtained from the parameter summary table printed after a fit or from the
model summary table printed after the MODEL command.
 category, the
category, the  covariate is equal to the value
of the continuous covariate for the subject, and all of the other covariates are
zero. If both variables in an interaction are categorical with
covariate is equal to the value
of the continuous covariate for the subject, and all of the other covariates are
zero. If both variables in an interaction are categorical with 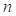 and
and  levels, respectively, a total of
nm covariates are added to the model. For a subject in which the first
categorical variable has the value
levels, respectively, a total of
nm covariates are added to the model. For a subject in which the first
categorical variable has the value  and the second
and the second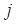 , the
, the 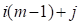 covariate is 1 and the remaining
covariate is 1 and the remaining
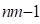 are zero. The indicator
variables used when a categorical variable is included in a fit are created for
each subject as the model is fit. Since these covariates do not use any of the
data workspace, they will be called virtual covariates. The names for virtual
covariates are generated by the programs. These names include the categorical
variable name and a numeric suffix that indicates the level.
are zero. The indicator
variables used when a categorical variable is included in a fit are created for
each subject as the model is fit. Since these covariates do not use any of the
data workspace, they will be called virtual covariates. The names for virtual
covariates are generated by the programs. These names include the categorical
variable name and a numeric suffix that indicates the level.