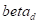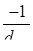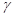BOUNDS
Purpose
Computes likelihood-based confidence bounds for the parameters
in a fitted model.
Syntax
BOUND pnum { LEVEL value }
{ UPPER
| LOWER | BOTH }
{ STEP value }
{ GOAL value }
{ PARA }
{ START nval }
{ FORCE }
{ PROFILE }
@
Arguments and Subcommands
pnum
The number of the parameter for which a likelihood ratio bound
is to be computed.
LEVEL value
Specifies the (two-sided) confidence level (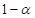 ) for confidence intervals. The
specified level should be a number between 50 and 100. Other values will be
ignored. This sets a global level which will also be used for bounds produced by
the CI command. The argument is truncated to the
nearest integer.
) for confidence intervals. The
specified level should be a number between 50 and 100. Other values will be
ignored. This sets a global level which will also be used for bounds produced by
the CI command. The argument is truncated to the
nearest integer.
UPPER
Requests only the upper bound. Once set, this option remains in
effect until explicitly changed.
LOWER
Requests only the lower bound. Once set, this option remains in
effect until explicitly changed.
BOTH
Requests both the upper and lower bounds. Once set, this option
remains in effect until explicitly changed. This is the default.
STEP value
Establishes value as the multiplier for the initial step
length. The algorithm used for likelihood bound computation determines the
parameter estimate by assuming that the likelihood is quadratic and taking a
step whose length is determined by the confidence level. The argument to this
subcommand is used to multiply the default step size. This is useful in cases in
which the likelihood is not very quadratic.
GOAL value
Causes the confidence level to be ignored. Instead, the
algorithm finds a parameter vector such that the deviance is equal to the
specified value. The value must be greater than the deviance for the
fitted model.
This feature is useful in the computation of a simultaneous
confidence region for two parameters. This can be done by fixing one of the
parameters of interest at some value and computing the bounds such that the
deviance is greater than the minimum deviance value by an appropriate amount.
For 95 percent bounds, the goal value should be 5.99 greater than the minimum
deviance for the model in which both parameters of interest are free. (5.99 is
the 95th percentile of the  distribution.)
distribution.)
PARA
Requests a printout of a parameter estimate table containing
information about the distance between the current likelihood and goal at each
iteration. The "deviance'' entry in this table contains the difference between
the deviance for the current fit and the value to be obtained at the bound of
interest. This value approaches zero as the bound is reached.
START nval
Specifies a starting value for the bound computations. When
this option is used the algorithm first fits a model with the parameter
constrained to equal the starting value and then uses the Moolgavkar-Venzon
algorithm to search for the bound. If nval is less than the maximum
likelihood estimate, only the lower bound is computed. If nval is greater
than the maximum likelihood estimate, only the upper bound is computed. The
START subcommand is especially useful for finding the
lower bound in models with implicit constraints on the parameter space, such as,
excess risk parameters that must be positive.
FORCE
forces computation of a bound for a fixed parameter. This is
useful when the maximum likelihood estimate occurs on a boundary of the
parameter space and you want to compute a one-sided bound. For example, in a
linear model for the relative risk of the form 1 + 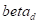 ,
,  must be greater than
must be greater than 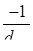 , where
, where  is the largest value of d. In
some cases, the best estimate may be obtained by fitting a model with
is the largest value of d. In
some cases, the best estimate may be obtained by fitting a model with  fixed at a value near
fixed at a value near  . One can obtain an approximate upper
bound using the command BOUND FORCE UPPER @.
. One can obtain an approximate upper
bound using the command BOUND FORCE UPPER @.
PROFILE
Use direct evaluation of the profile likelihood function to
determine the bounds rather than the .default Moolgavkar-Venzon (1987) to find
the bounds. This method is slower, but can be more robust in some
problems.
Remarks
The default is to start with the Moolgavkar-Venzon method
(1987) but to switch to the direct method if there are signs of trouble. When
the BOUNDS command is given, the value of the maximum
likelihood estimate for that parameter is saved as #_MLEST and the standard error of this parameter is saved as
#_MLESE. The new PROFILE
subcommand is illustrated in the AMEX1.AMF example.
The BOUNDS command computes
likelihood based bounds by direct exploration of the profile likelihood
function. This is done using a constrained Newton-Raphson algorithm similar to
that described by Moolgavkar and Venzon (1987). The search is quite efficient
and, in most cases, the amount of time required to compute each bound is roughly
equal to the time it takes to fit a new model. When successfully computed, the
likelihood bounds are stored in the named constants #_LRLO and #_LRHI.
Situations can arise in which a bound does not exist because of
constraints on the parameter space. In addition, bounds may be difficult to
compute when the likelihood, as a function of the parameter of interest, changes
slowly.
If the program indicates that a feasible bound cannot be found,
it is often a good idea to explore the likelihood directly using the PARAMETER command to fix the parameter of interest and the
FIT command to maximize the profile likelihood for the
indicated parameter value.
Problems in computing likelihood bounds are more commonly
encountered when searching for lower bounds. As noted above, when problems
occur, they are often caused by implicit or explicit constraints on the
parameter space. For example, an additive relative risk model parameterized as
 is equivalent to a model of the
form
is equivalent to a model of the
form  , with the restriction that
, with the restriction that  . Thus, there would be no feasible
lower bound for
. Thus, there would be no feasible
lower bound for  whenever the value of
whenever the value of 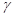 at the lower bound was negative.
Another situation in which the program will fail to find a lower bound occurs
when certain parameter values lead to negative risks.
at the lower bound was negative.
Another situation in which the program will fail to find a lower bound occurs
when certain parameter values lead to negative risks.
Options set using the LEVEL, UPPER, LOWER, and BOTH subcommands are "sticky'' in the sense that they remain
in effect until changed by the user or the session ends.
Examples
a) To find the
bound for parameter 6 using the the Moolgavkar- Venzon algorithm:
BOUND 6 @
b) To find only a
90% upper bound for parameter 6 using direct evaluaton of the likelihood:
BOUND 6 PROFILE UPPER LEVEL
90
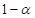 ) for confidence intervals. The
specified level should be a number between 50 and 100. Other values will be
ignored. This sets a global level which will also be used for bounds produced by
the CI command. The argument is truncated to the
nearest integer.
) for confidence intervals. The
specified level should be a number between 50 and 100. Other values will be
ignored. This sets a global level which will also be used for bounds produced by
the CI command. The argument is truncated to the
nearest integer.